Intuitive Explanation of Group LASSO Regularization for Neural Network Interpretability
03 Aug 2020Neural networks are often referred to as a black box model because of its lack of interpretability. Most of a network’s operations occur in the hidden layers and latent space. As a result, tracing important features in a dataset is not an easy task, especially when the number of features is large. This is often a limiting factor in applying neural networks in fields where explainability is not only favored, but crucial (such as medical diagnostics or finance).
Through this entry, we hope to examine the application of the group LASSO regularization for solving the problems described above.
What is ridge and LASSO regularization?
The loss function of ridge regression can be defined as
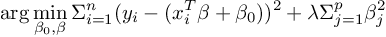
while loss function of LASSO regression can be defined as
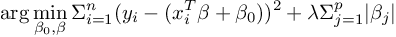
The above loss functions can be broken down into
- Predicted output:
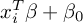
- Regularization term
for LASSO
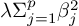for ridge
Comparison of the two regularization terms shows the intuition behind LASSO regression’s better interpretability characteristics. From a Big-O standpoint,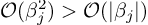 
. The penalty for having one skewed large value is much greater for ridge regression. Ridge regularization aims to reduce variance between the coefficients, therefore driving all features down to zero.
LASSO regularization, on the other hand, will set some feature’s coefficients to zero values when deemed necessary, effectively removing them. We then can compare non-zero coefficients to determine the importance of the features.
What is group LASSO regularization?
From the above example, we observe how LASSO regularization can help with the interpretability of the model. But some problems may benefit from a group of features used together, especially when incorporating domain knowledge into the model.
Group LASSO attempts to solve this problem by separating the entire feature set into separate feature groups. The regularization function can be written as
where
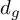denotes the size of the group.
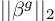denotes the L2-norm of the feature group 
.
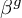Let’s take a closer look at the regularization term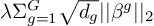 
.
Note that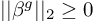 
, and we for some 
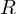that satisfies 
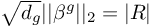, we could effectively rewrite the equation as
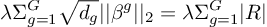
In this case, we have effectively reduced the regularization to LASSO regularization on the inter-group level.
Similarly, let’s take a look an subgroup. Expanding the term for some group with cardinality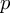 
, the regularization term can be expressed as
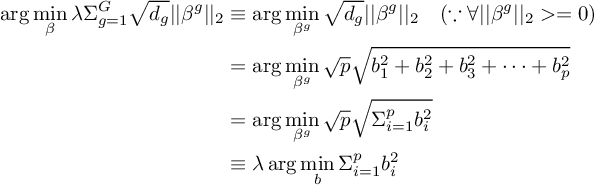
Here, we have effectively reduced the regularization to ridge regularization on the intra-group level.
We build on the intuition that while it cannot select certain features within the same group, because of it’s LASSO-like nature between feature groups, the model will zero-out entirety of certain coefficient groups.
Additionally, note the two following characteristics:
- When
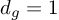, the regularization term essentially becomes a LASSO (L1) regularization. - When
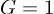, the regularization term essentially becomes a ridge (L2) regularization.
How can we adapt group LASSO for neural networks?
Up to now, the application of regularization terms have been on linear regression methods where each features are assigned a single coefficient weight. Now, we will take a look at a neural network, specifically on the connections between the first two layer of the network, where each individual features have multiple weights associated to the next layer.
To visualize this, say we have a small neural network with one hidden layer.
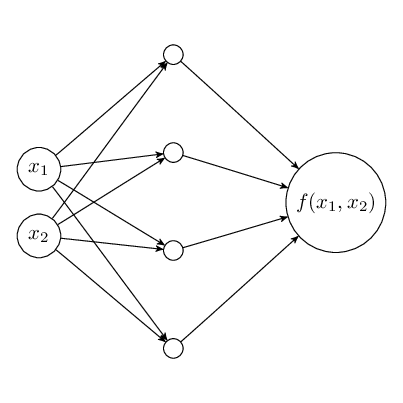
In order for the above feature selection to work, we will need to zero out the weights connected for all of feature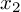 
(marked in red).
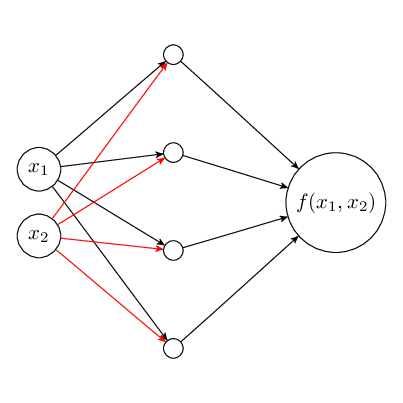
In this case, the weights associated with each of the neurons becomes becomes a group of their own. Let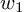 
and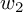 
denote the weight vectors for input features 
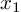and 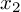( 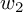weights would be marked in red above). We can adapt the group LASSO regularization formulation as
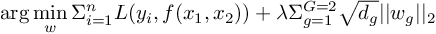
where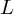 
denotes the loss function and 
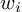denotes the full-connected weights to feature 
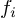. Since we have two input features, the regularization term would also expand to
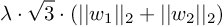
We have essentially derived the Group level lasso regularization on each of the individual features, with the weights corresponding to each feature in a group. We can continue to build on the intuition from the Group LASSO.
While each individual weights inside a weight group will not differ in terms of convergence to zero (all elements of 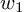, 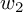will either be zero or non-zero), the non-continuous nature of the l2 norm for individual features will introduce sparsity and converge entire feature weights to 0.
From here, it’s trivial to apply the same technique to regularizing hidden layers to introduce further sparsity to the model and improve model capacity or prune unneeded connections.